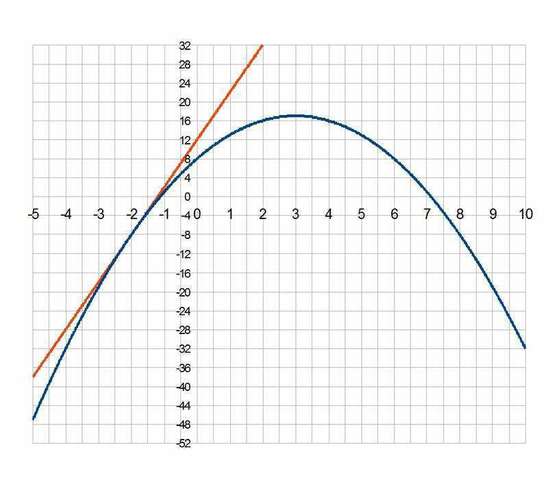
касательнaя ест просто производной в точке
потому решаем производную.
f ' (x) = (-x^2 )' + (6x)' + (8)' = (-2)x + 6 + 0 = 6 - 2x
f '(-2) = 6 - 2(-2) = 10
тут красиво видно почему то производную по иксе записываем тоже так
df(x) / dx значит: сколко изменилос функции до изменения икса
решене число 10 = df(x) / dx = tg ( угла касателной )
значит это А в уровнению прямой : y= Ax+B
оттуда знаем что наша касательная иммеет уровнение y = 10x +B
искана касателная имеет в точке такие значениe как дана функция
f(-2) = f ' (-2) = -(-2)^2 + 6(-2) + 8 = -4 - 12 + 8 = (-8)
вернуемся к касателно, решаем число B
y =10x + B ; y = -8 ; x= -2
-8 = 10(-2) + B
-8 = -20 + B
B = -8 +20 = 12
уровнение касательной :
y = 10 x +12
сделаем граф - во вложению