Произведение двух множителей равно 0 тогда и только тогда когда хотя бы один из них равен 0, а другой при этом не теряет смысла.
ОДЗ: 2016-x²≥0 ⇒ x∈[-√2016;√2016]
1) 2016-x²=0 - два корня х=-√2016 и х=√2016
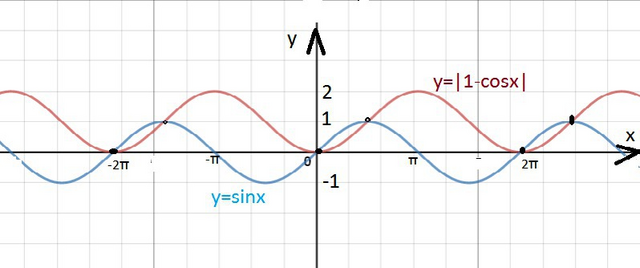
2) |1-cosx|-sinx=0
|1-cosx|=sinx
1-cosx≥0 при любом х.
Уравнение имеет решение при sinx≥0
1-cosx=sinx
sinx+cosx=1
Делим все уравнение на √2 и применяем метод вспомогательного угла
sin(x+(π/4))=√2/2.
х+(π/4)=(π/4)+2πk, k∈Z.
x=2πk, k∈Z
или
х+(π/4)=(3π/4)+2πn, n∈Z.
х=(π/2)+2πn, n∈Z.
На отрезке длиной 2π≈6,28 два корня.
На промежутке [0; √2016) 15 корней.
√2016≈44,89
44,89:6,28=7,14
14 корней на [0; 7·6,28) плюс корень 7·6,28. Всего 15
и симметрично слева 15 корней.
О т в е т. 32 корня.