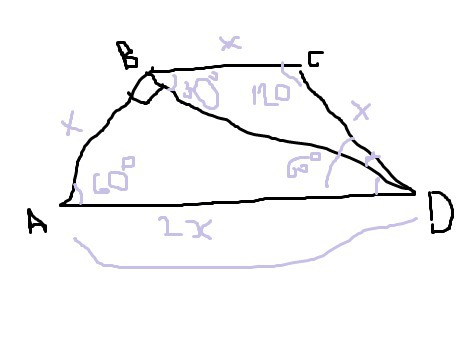
Я надеюсь, что чертеж не совсем непонятный))
Итак, мы нарисовали трапецию ABCD обозначили на ней все углы.
Рассмотрим треугольник ABD. Угол абд равен 90, т.к. бд перпендикулярна аб. И угол адб равен 30 по условию. Этот треугольник прямоугольный. Значит угол А будет 60 градусов.
Рассм. угол Д. Он состоит из адб и бдс, это 30+30=60.
Т.к. угол А и угол Д равны, то этот треугольник равнобедренный и АБ и СД равны.
Далее вспомним еще одно свойство прямоугольного треугольника. катет, лежащий напротив угла в 30 градусов, равен половине гипотенузы.
_____________________________________________
Периметр равен сумме 4-х сторон. Поэтому мы обозначим наши стороны иксами. Так аб и сд, как равные, обозначим "x" и гипотенузу прямоугольного треугольника, ад, как "2x". Нам осталось найти верхнюю сторону, бс.
_____________________________________________
Т.к. это равнобедренная трапеция, то и верхние углы равны, значит:
Б=С=180-60=(360-60-60):2=120
Рассм. треугл. бсд. Угол дбс = 30 градусов, т.к. угол Б-абд=120-90=30.
Угол бдс тоже равен 30 (по условию).
Следовательно, треугольник бсд равнобедренный, и значит, что бс=сд=x
______________________________________________
Итак, наше P = x+x+x+2x=5x
x=60/5x=12
AD=2x=12*2=24 cm.
Ответ: AD = 24 см.