В основании пирамиды лежит прямоугольный треугольник,один из катетов которого равен...

Question

В основании пирамиды лежит прямоугольный треугольник,один из катетов которого равен 6см.Все боковые рёбра равны 13.Высота пирамиды равна 12см.Вычислите второй катет этого треугольника

Answer 1

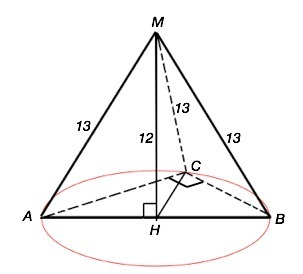
Обозначим пирамиду МАВС. СВ=6 см

Высота ВН перпендикулярна плоскости основания, поэтому треугольники, образованные боковыми ребрами, высотой и проекциями ребер,  прямоугольные. В данном случае отношение их сторон из троек Пифагора (5:12:13), поэтому проекции боковых ребер равны 5 ( можно и по т.Пифагора найти). 

АН=СН=ВН ⇒ основание высоты  МН пирамиды является центром описанной окружности ∆ АВС с радиусом, равным 5, ⇒

 гипотенуза АВ=2R=10 см. 

По т.Пифагора ( или из отношения СВ:АВ=3:5) находим АС=8 см, это второй катет ∆ АВС. 

---