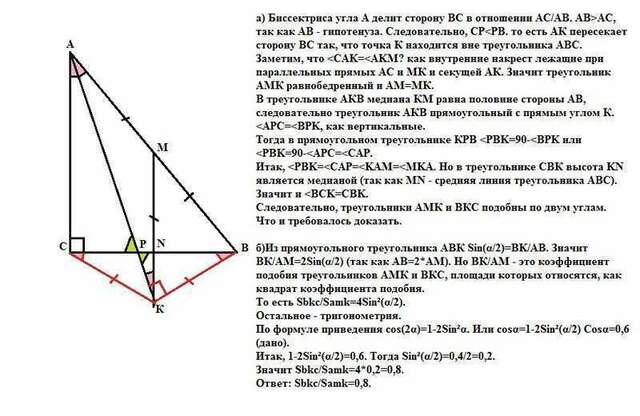
А) Биссектриса угла А делит точкой Р сторону ВС в отношении АС/АВ. (свойство биссектрисы).
АВ>AC, так как АВ - гипотенуза. Следовательно, СРЗаметим, что В треугольнике АКВ медиана КМ равна половине стороны АВ, следовательно треугольник АКВ прямоугольный с прямым углом К.
Тогда в прямоугольном треугольнике КРВ: Итак, Следовательно, треугольники АМК и ВКС подобны по двум углам.
Что и требовалось доказать.
б)Из прямоугольного треугольника АВК Sin(α/2)=BK/AB. Значит ВК/АМ=2Sin(α/2) (так как АВ=2*АМ). Но ВК/АМ - это коэффициент подобия треугольников АМК и ВКС, площади которых относятся, как квадрат коэффициента подобия.
То есть Sbkc/Samk=4Sin²(α/2).
Остальное - тригонометрия.
По формуле приведения cos(2α)=1-2Sin²α. Или cosα=1-2Sin²(α/2) Cosα=0,6 (дано).
Итак, 1-2Sin²(α/2)=0,6. Тогда Sin²(α/2)=0,4/2=0,2.
Значит Sbkc/Samk=4*0,2=0,8.
Ответ: Sbkc/Samk=0,8.