Исследовать функцию с помощью первой и второй производных. f(x)=6-x^2-x^3 Построить...

0 голосов
42 просмотров

Исследовать функцию с помощью первой и второй производных.

f(x)=6-x^2-x^3

Построить график.

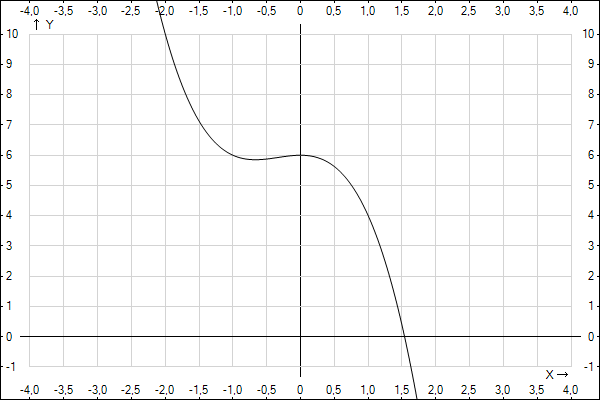
image
Математика (15 баллов) | 42 просмотров
Дан 1 ответ
0 голосов
Правильный ответ

f(x) = 6-x^2-x^3\\ f'(x) = -2x-3x^2\\ f''(x) = -2-6x

 

Рассмотрим первую производную

она имеет два корня:

-2x-3x^2 = 0\\ x(3x+2) = 0\\ x_1 = 0; x_2 = -\frac{2}{3}

между корнями производная положительна - функция возрастает, вне этого отрезка производная отрицательна - функция убывает...

 

Теперь рассмотрим вторую производную:

она обращается в 0 в одной точке (точка перегиба)

-2-6x=0\\ x_0 = -\frac{1}{3}

 

График функции во вложении

 

image
(11.5k баллов)
Похожие задачи