❤❤❤❤❤❤❤❤❤❤❤❤ПОМОГИТЕ ПОЖАЛУЙСТА!)❤❤❤❤❤❤❤❤❤❤❤❤ 1.Дан треугольник ABC , точка М лежит **...

Question

❤❤❤❤❤❤❤❤❤❤❤❤ПОМОГИТЕ ПОЖАЛУЙСТА!)❤❤❤❤❤❤❤❤❤❤❤❤
1.Дан треугольник ABC , точка М лежит на АВ, точка К лежит на ВС и ВМ : МА = 3:4
Через прямую МК проходит плоскость α паралл. прямой АС
а) Док-ть , что ВС : ВК = 7 : 3
б) Найти длину МК , если АС = 14 см.

2.Дан треугольник АВС , точка Е лежит на АВ , точка К лежит на ВС
ВЕ/ВА = ВК/ВС = 2/5
Через прямую АС проходит плоскость α, не совпад. с плоскостью треугольника АВС
а) Док-ть ЕК║α
б) Найти АС , если ЕК=4 см

Answer 1

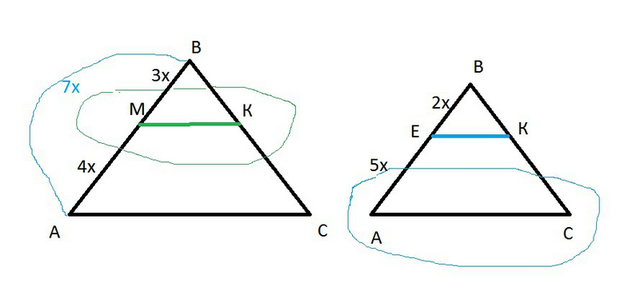
1) Плоскость, параллельная прямой АС, пересекает плоскость треугольника АВС по прямой, параллельной АС.
Значит, Δ МВК подобен ΔАВС ( МК || AC).
Пусть ВМ =3х, МА = 4х, тогда ВМ : МА = 3х : 4х = 3 : 4.
АВ=3х+4х=7х
Из подобия Δ МВК и  ΔАВС
ВС:ВК=МВ:АВ=7x:3x=7:3,
ВС:ВК=АС:МК  = 7:3
МК=АС·(3/7)=14·(3/7)=6 см.

2)ВЕ/ВА = ВК/ВС = 2/5 ⇒ по теореме, обратной теореме Фалеса
 ЕК || AC
Если плоскость проходит через прямую параллельную другой прямой, то плоскость и другая прямая параллельны.
Значит, Δ ВЕК подобен ΔВАС ( ЕК || AC).
Из подобия
ВЕ:ВА=ЕК:АС=2:5
АС=ЕК·(5/2)=4·(5/2)=10 см

---