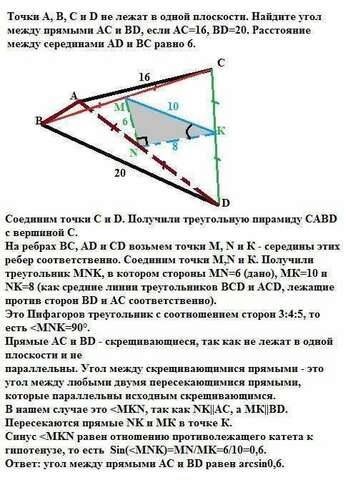
Соединим точки С и D. Получили треугольную пирамиду САВD с вершиной С.
На ребрах ВС, АD и СD возьмем точки М, N и К - середины этих ребер соответственно. Соединим точки M,N и К. Получили треугольник MNK, в котором стороны MN=6 (дано), МК=10 и NK=8 (как средние линии треугольников ВСD и АСD, лежащие против сторон ВD и АС соответственно).
Это Пифагоров треугольник с соотношением сторон 3:4:5, то есть Прямые АС и ВD - скрещивающиеся, так как не лежат в одной плоскости и
не параллельны. Угол между скрещивающимися прямыми - это угол между любыми двумя пересекающимися прямыми, которые параллельны исходным скрещивающимся.
В нашем случае это Пересекаются прямые NK и МК в точке К.
Синус Ответ: угол между прямыми АС и ВD равен arcsin0,6.