1) сначала найдем область определения функции и приведем ее к наиболее простому виду. у=1/ [x]. Отсюда следуетЮ что у всегда будет положительным.
Однако стоит помнить, что знаменатель никогда не равен нулю - поэтому 2[х^2]-[x] так же не равно нулю. Приравниваем к нулю и смотрим, чему не может быть равен х.(он не равен 0;0,5;-0,5).
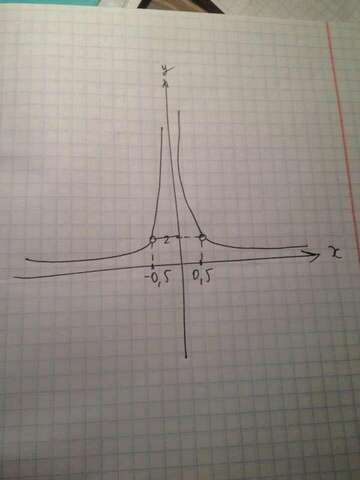
2) Графиком функции у=1/[x] является гипербола, расположенная в 1 и 2 четвертях с выколотыми точками, где график не будет существовать. Определим у для каждой из таких точек( х мы определили в пункте 1).
х 0.5 -0.5
у 2 2.
(см. рисунок)
3) теперь определим значения k, при которых прямая не имеет общих точек с графиком.
Значит, она должна проходить через точки (0.5;2) или (-0.5;2).
подставим значения х и у в уравнение(у=kx), чтобы найти k:
1)2=k*0.5 => k=4
2)2=k*(-0,5) => k=-4.
Ответ: прямая не имеет с графиком общих точек при k=4; k=-4.