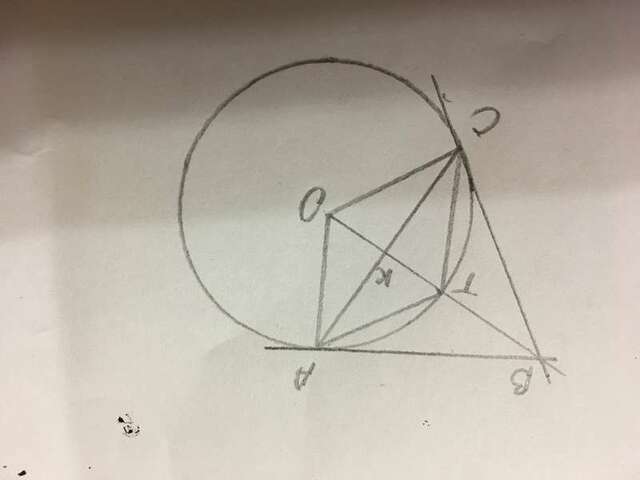Прямые ВА и ВС - касательные к окружности, центром которой является точка О, точки А и С...

Question

Прямые ВА и ВС - касательные к окружности, центром которой является точка О, точки А и С - точки касания. Окружность пересекает отрезок ОВ в точке Т, угол АТС = 120 градусов. Докажите, что точка Т является точкой пересечения биссектрис ∆ АВС.
Пожалуйста напишите хороший ответ с объяснением.

Answer 1

Касательные к окружности, проведённые из одной точки, равны. ВА=ВС, значит тр-ник АВС - равнобедренный. 
ΔАВО=СВО потрём сторонам (АВ=ВС, АО=СО=R, ВО - общая сторона), значит ∠АВО=∠СВО ⇒ ВО - биссектриса угла В.
Угол, вписанный в окружность, равен половине градусной меры дуги, на которую он опирается, значит большая дуга АС равна: ∩АС=2∠АТС=2·120=240°.
∠АОС=360-∩АС=360-240=120°.
В равнобедренных тр-ках АСТ и АСО  углы при вершинах равны 120°, значит углы при основаниях тоже равны. ∠ТАС=∠ОАС=(180-120)/2=30°.
∠ВАС=∠ВАО-∠ОАС=90-30=60°.
∠ВАС=60°, ∠ТАС=30°, значит АТ - биссектриса.
ΔВАК=ΔВСК, т.к. ВА=ВС, ВК - общая и ∠АВК=∠CВК, значит СТ=АТ ⇒ СТ - биссектриса.
В тр-ке АВС ВК, АТ и СТ - биссектрисы его углов.
Доказано.

---

Comments

Спасибо!

---

http://znanija.com/task/20338750

---

трите пожалуйста еще здесь задачу

---

СПАСИБО!