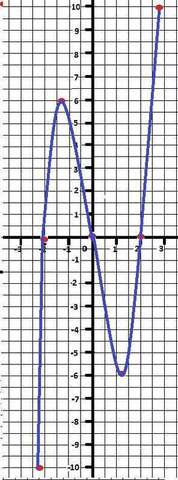
Исследование функции Y =x³-8x.
1. Область определения - Х⊂(-∞,+∞).
2. Пересечение с осью абсцисс
2Х*(Х²-4)=0
Х1 = 0, Х2 = -2, Х3 = 2.
3. Пересечение с осью ординат
Y(0) = 0.
4. Предельные значения.
Lim(-∞) = -∞
Lim(+∞) = +∞
5. Исследование на четность.
Y(-1) = -(Y(1) - функция нечетная.
6. Монотонность.
Производная функции
Y' = 6x² - 8.
Корни производной - точки экстремума.
х1 = -2/√3 х2 = 2/√3.
Возрастает: Х⊂(-∞, -2/√3]∪[2/√3,+∞)
Убывает: [-2/√3,+2√3].
7. Ymax(-2/√3) = +6 Ymin(2/√3) = -6.
8. Область допустимых значений: Y⊂(-∞,+∞).
Эскиз графика в приложении.