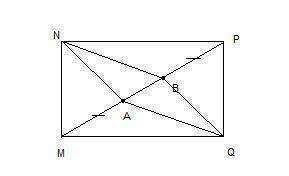
Дано: MNPQ - прямоугольник
MP - диагональ
МА = РВ
Доказать: ANBQ - параллелограмм.
Доказательство:
1.Рассмотрим треугольники PBN и MAQ.
Они равны по двум сторонам и углу между ними:
PN=MQ как противоположные стороны прямоугольника
ВР=АМ по условию
уголNPM=уголQMP (как накрест лежащие углы при пересечении двух параллельных прямых PN и MQ секущей МР.)
Из равенства треугольников следует, что их стороны AQ=BN
2.Рассмотрим треугольники PBQ и MAN. Они равны по двум сторонам и углу между ними:
PQ=MN как противоположные стороны прямоугольника
ВР=АМ по условию
Из равенства треугольников следует, что их стороны BQ=AN
Используя признак параллелограмма о том, что, если в четырехугольнике противоположные стороны попарно равны (AQ=BN и BQ=AN), то этот четырехугольник - параллелограмм, делаем вывод, что ANBQ - параллелограмм, что и требовалось доказать!