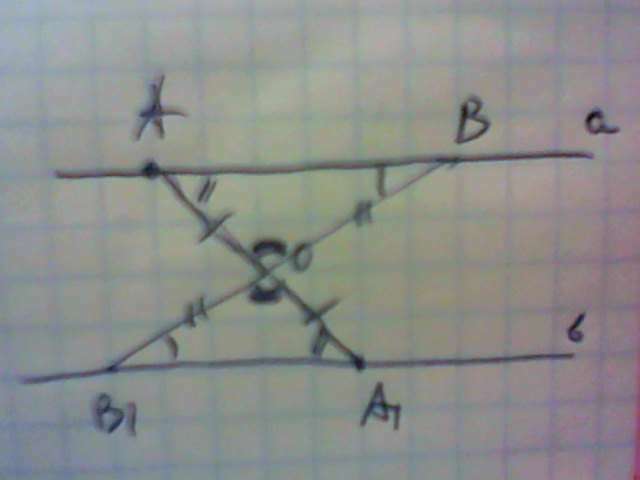
479.а) Начнем с построения рисунка. изобразим по своему усмотрению прямую а.Возьмем точку О, которая не лежит на этой прямой и примем ее за центр симметрии. Обратите внимание, что точка и прямая были выбраны произвольно.
Возьмем на прямой а произвольную точку А и построим симметричную точку А1: соединим точку А с центром симметрии О и продолжим прямую на расстояние равное ОА; найденную таким образом точку обозначим А1, ОА=ОА1.
Возьмем на прямой а другую точку В и построим дл нее симметричную точку В, таким же способом как и строили точку А1 .
Через две полученные точки проведем прямую b.
Чтобы доказать , что а║b, необходимо рассмотреть ΔАОВ=ΔА1ОВ1 (две стороны одного треугольника равны двум сторонам другого треугольника по построению и вертикальные углы прямые. А дальше рассматриваем утверждение "если две прямые пересекаются третьей прямой (секущей) и при этом разносторонние навкрест лежащие углы равны, то прямые а и b параллельные.Как видите, доказательство очень длинное. Проще было бы через скайп. Попробуйте.