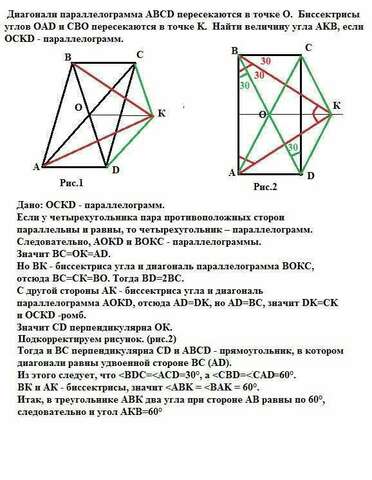
Дано: ОСКD - параллелограмм.
Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.
Следовательно, АОКD и ВОКС - параллелограммы.
Значит ВС=ОК=АD.
Но ВК - биссектриса угла и диагональ параллелограмма ВОКС, отсюда ВС=СК=ВО.
Тогда ВD=2ВС.
С другой стороны АК - биссектриса угла и диагональ параллелограмма АОКD, отсюда АD=DK, но АD=ВС, значит DK=CK и ОСКD -ромб.
Значит СD перпендикулярна ОК.
Подкорректируем рисунок (рис.2)
Тогда и ВС перпендикулярна СD и АВСD - прямоугольник, в котором диагонали равны удвоенной стороне ВС(АD).
Из этого следует, что ВК и АК - биссектрисы, значит Итак, в треугольнике АВК два угла при стороне АВ равны по 60°, следовательно и угол АКВ=60°.
Ответ: угол АКВ = 60°.