Решите ,пожалуйста , хоть 1 билет

Question

Решите ,пожалуйста , хоть 1 билет

---

Answer 1

Билет 7
1.1) у ромба все стороны равны ,
2) противоположные углы равны,
3) диагонали ромба являются биссектрисами углов из которых они исходят,
4) противоположные стороны параллельны
2.
Или так: пусть E -- точка пересечения диагоналей. Треугольники AEB и CEB равны, по двум сторонам и углу: 1) по условию задачи, углы AEB=BEC=90 градусов, 2) сторона EB у них общая, и 3) AE=EC, потому что E делит AC пополам (иначе не прямоугольник) . Из равенства треугольников следует, что AB=BC. Раз прямоугольник, то AB=CD, и BC=AD. Значит, из только что доказанного AB=BC следует AB=BC=CD=DA. Стало быть, квадрат
3.с этим Вы сами разберетесь
4.6 см

Answer 2

Билет 6.
1.Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
У параллелограмма противолежащие стороны равны.
У параллелограмма противолежащие углы равны.

2. Доказываем через треугольники, образованные диагоналями, у которых основания - боковые стороны трапеции. Так как диагонали равны, то и боковые стороны треугольников между собой равны, а углы при вершине у центра трапеции вертикальные, следовательно по признаку равенства треугольников (две стороны и угол между ними) они равны, а значит основания у них равны, из чего следует, что трапеция равнобедренная.

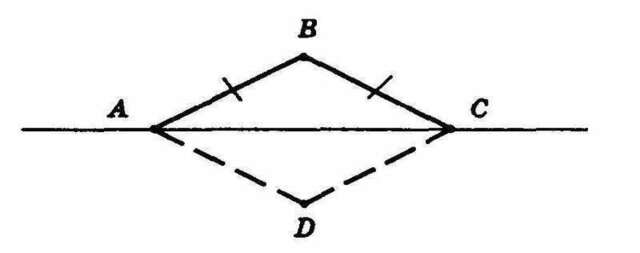
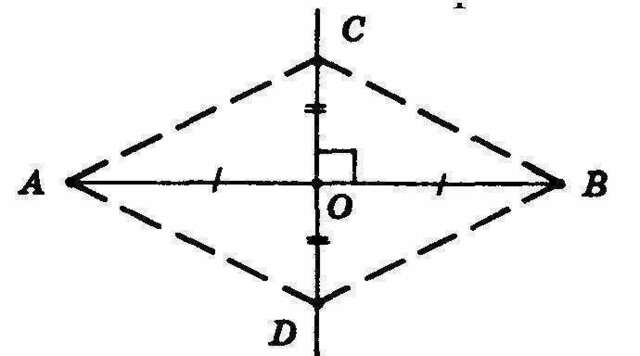
3.1) Построим диагональ АС. Строим треугольник АВС по трем сторонам АВ, ВС, АС, где АВ = ВС — данные стороны ромба, а АС — диагональ ромба. Через точку А проводим прямую, параллельную ВС, а через точку С прямую, параллельную АВ. Точку пересечения данных прямых обозначим D ABCD - искомый ромб.

---

---