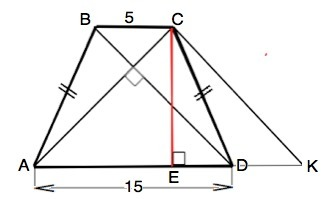
Как видно из рисунка, данного в приложении к вопросу, трапеция равнобедренная.
Если в равнобедренной трапеции диагонали пересекаются под прямым углом, её высота равна полусумме оснований ( средней линии)- свойство.
Подробно:
Рассмотрим равнобедренную трапецию АВСD, АС⊥ВD
Проведем через вершину С параллельно АВ прямую до пересечения с продолжением АD в точке К.
Четырехугольник ВСКD - параллелограмм ( ВС║АК по условию, СК║ВD по построению). Следовательно, DК=ВС=5.
В равнобедренной трапеции диагонали равны.
Так как СК║ВD, ∠АСК =∠АОD как соответственный при пересечении параллельных прямых секущей.
Следовательно, треугольник АСК прямоугольный равнобедренный, его высота, как высота равнобедренного треугольника, является его медианой, а острые углы равны 45°, и ∆ АС=∆ КСЕ с общим катетом СЕ.
(Медиана прямоугольного треугольника равна половине гипотенузы)
Значит, СЕ=АЕ=ЕК.
АD+DK=15+5=20
CE=20:2=10 см