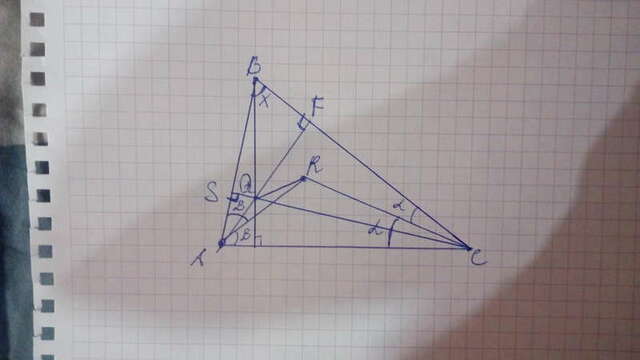
Смотрите рисунок.
Начнем с того, что раз треугольник остроугольный,то все высоты находятся внутри треугольника,то внутри расположен и сам ортоцентр.
Пусть R центр вписанной окружности,тогда он есть пересечение биссектрис. То есть AR и CR биссектрисы углов C и A.
Пусть разбитые ими углы равны
Альфа и Бетта. А угол B=x.
Q-ортоцентр ,то есть AF и CS высоты к сторонам BC и AB.По условию выходит что четырехугольник AQRC вписан в окружность,значит углы: QAR=QCR,как углы опирающиеся на общую дугу QR. Из рисунка видно что: QAR= Бетта -(90-x).
CQR=Альфа-(90-2*Бетта).
Откуда: Бетта+x=Альфа +2*Бетта
x=Aльфа+Бетта.
Из того что сумма углов треугольника ABC равна 180 имеем: x+2*Альфа+2*Бетта=180
3x=180
x=60. Ответ: x=60