ДАНО
А(3;-1), В(1;4), С(5;-10)
НАЙТИ
Уравнения сторон треугольника.
РЕШЕНИЕ
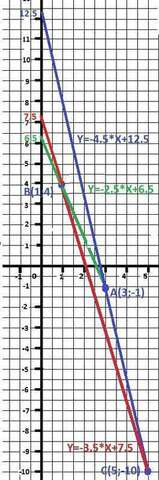
Для удобства представления задачи чертим этот треугольник на координатной плоскости.
Уравнение прямой проходящей через две точки (А и В) пишем в виде
Y = k*X + b, где:k - коэффициент наклона, b - сдвиг по оси Y.
k = ΔY/ΔX = (Ay-By)/(Ax-Bx) = (-1 - 4)/(3-1) = -5/2 = -2.5
Сдвиг b найдем из условия, что прямая проходит через данную точку, например, точку А(3;-1).
Ay = k*Ax + b, отсюда
b = Ay - k*Ax = -1 - (- 5/2)*3 = -1 + 7.5 = 6.5
Окончательно уравнение прямой АВ
Y(AB) = - 2.5*X + 6.5 - ОТВЕТ - зеленая линия.
Аналогично для прямой СВ.
k = (-10- 4)/(5-1) = -14/4 = - 3.5
Сдвиг определим по точке В(1;4)
b = 4 - (-3.5)*1 = 7.5
Окончательно уравнение СВ
Y(CB) = - 3.5*X+7.5 - ОТВЕТ - красная линия
И уравнение прямой АС
k = (-10-1)/(5-3) = -9/ = - 4.5.
Сдвиг b для точки А.
b = - 1 + 4.5*3 = 12.5
окончательно уравнение прямой АС.
Y(AC) = - 4.5*X + 12.5 - ОТВЕТ - синяя линия.