В правильной треугольной пирамиде сторона основания равна 15√3 см , а боковое ребро - 17...

Question

В правильной треугольной пирамиде сторона основания равна 15√3 см , а боковое ребро - 17 см . Вычислить площадь сечения , проведённого через боковое ребро
и высоту пирамиды

Answer 1

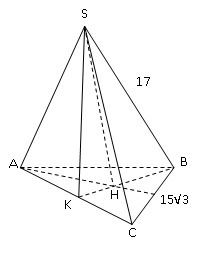
SABC-правильная пирамида, сечение проходит через ребро, высоту и середину противоположной стороны: ΔBSK-нужное сечение.
S=0,5*BK*SH
1) ΔABC: BK⊥AC, BK=AC√3/2=15√3*√3/2=45/2 (см).
2) ΔSHB-прямоугольный, SB=17 см, HB=2/3BK=2/3*45/2=15 (см),
из т.Пифагора следует, что SH=√SB^2-BH^2=√289-225=√64=8 (см).
S=0.5*45/2*8=90 (кв.см).
Ответ: 90 кв.см. 

---

Comments

А как в последнем решении получилось 90? ( подсчеты )

---

45/2=22,5

---

0,5*22,5*8=90

---

Спасибо , не правильно знаки понял .