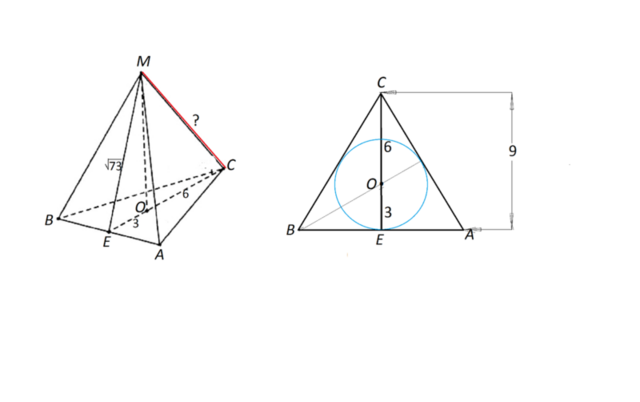
Пусть дана пирамида МАВС, и
высота её основания СЕ=9
Высота боковой грани МЕ=√73
Основание высоты правильной пирамиды находится в центре О вписанной окружности, т.е. в точке пересечения биссектрис, высот, медиан правильного треугольника.
Эта точка по свойству медиан делит их в отношении 2:1, считая от вершины.
Следовательно, ОЕ равно 1/3 СЕ.
ОЕ=9:3=3
ОС=9-3=6
По т.Пифагора высота пирамиды:
МО=√(МЕ²-ОЕ²)=√64=8
Боковое ребро:
МС=√(МО²+ОС²)=√100=10
---
[email protected]