Найдите периметр данного параллелограмма.

Question

Найдите периметр данного параллелограмма.

---

Comments

А углы зачем помечены в задании? Их самим мерять? Потому что если углы известны - решить можно, а если нет, то - нельзя.

---

Мерить не нужно, задание отправили по электронной почте. Больше никаких данных и пояснений нет.

---

Но углы зачем-то помечены. Если знать угол BCF , например, можно найти сторону BC через угол и противолежащую сторону. Затем найти длину отрезка FA, составив пропорцию, где 8/FA=BC/5 - на основании того, что треугольники FBC и FAK подобны. Затем сложить 8 с FA, получив длину BA. А затем сложить ВА и BC и умножить на 2, получив периметр... По другому решить невозможно. Уточните, нужно ли мерить углы.

---

Я измерил в фотошопе - у меня получился угол BCF приблизительно равен 54градуса. Но, скорее всего, картинка искажена про съёмке, а в настоящей картинке задания это угол = 55 градусов. Дальше надо найти формулу вычисления треугольника по углу и противолежащей стороне (8 см). А дальше всё - по предыдущему моему комментарию.

Answer 1

Если измерить помеченные на рисунке угла, то ∠ BCF≈55° , а ∠ KCD≈60°.
Δ BFС и Δ KCD - подобны, поэтому соответствующий углу KCD ∠ BFC= 60° тоже.
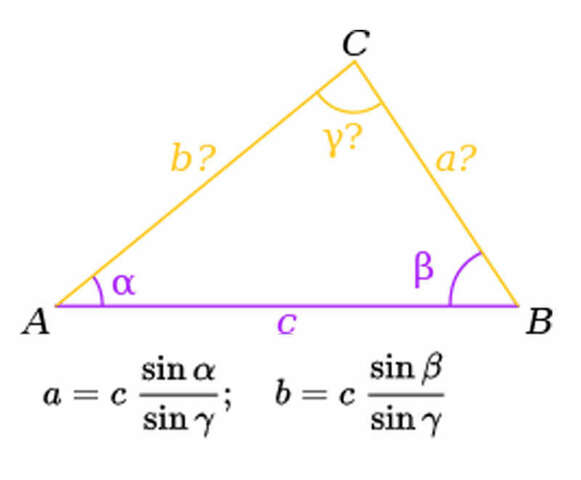
Таким образом мы знаем достаточно, чтобы применить формулу вычисления треугольника по 2м углам и стороне (см. приложенную картинку). 
ВС=8 × (sin 60°/ sin 55°) ≈ 8,458 см
Далее находим длину FA, исходя из подобия Δ BCF и Δ FAK. Cторона BC соответствует стороне KA, равной 5 см.
Составляем пропорцию: 
8 / FA = 8,458 / 5
FA≈ 4,734 см
Далее находим длину ВА=BF+FA=8+4,734=12,734 см
Далее мы, наконец, можем найти периметр параллелограмма.
Р= 2×(ВС+BA)≈ 42,376 см 

Приблизительно (≈) , потому что все углы и найденные стороны вычислены и измерены приблизительно. На самом деле в данном решении все знаки равно можно писать волнисто, так как точных углов мы не знали, а измеряли и округляли полученный результат.

---

Comments

Просьба к модераторам - не удалять решение из-за картинки, так как картинку я создал сам в фотошопе. А ваш сайт ругается, что она скопирована, что является неверной оценкой данной картинки.