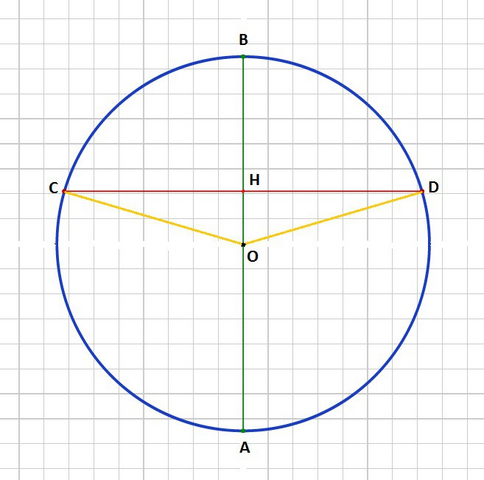
Найдём диаметр окружности, он равен сумме АН и ВН:
d=AH+BH=9,6+5,4=15
Зная диаметр можем найти радиус:
r=d/2=7,5
Рассмотрим треугольник ОСН. Этот треугольник прямоугольный так как хорда CD пересекает диаметр под прямым углом. Точка О - центр окружности, угол ОНС - прямой, сторона ОС - радиус окружности.
Найдём длину стороны ОН.
ОН=ОВ-ВН
ОВ=7,5 - радиус окружности, а ВН=5,4
ОН=7,5-5,4=2,1
Теперь по теореме Пифагора можем найти СН
СН²=ОС²+ОН²
СН²=7,5²+2,1²=56,25+4,41=60,66
СН=√60,66=√9*6,74=3√6,74
Так как хорда пересекает диаметр под прямым углом, то СН=НD, следовательно
CD=2CH=2*3√6,74=6√6,74