помогите пожулуйста решить задачу по геометрии! ЭТО ОЧЕНЬ ВАЖНО! 9 класс в треугольнике...

Question

Дано ответов: 2

Правильный ответ

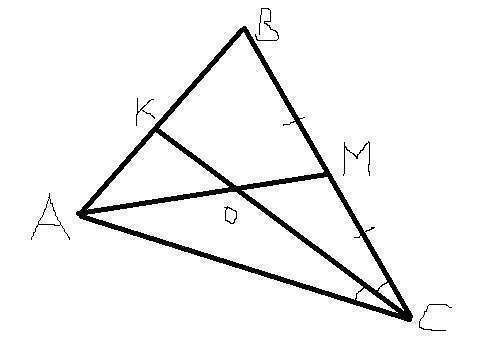
Обозначим точку пересечения АМ и CK через О. Рассмотрим треугольник АBС.

Есть такая формула для нахождения длины биссектрисы.

$l=\frac{2ab\cos\frac{\gamma}{2}}{a+b},$

где a, b - стороны треугольника, к которым относится биссектриса, а $\gamma$ - угол между этими сторонами.

Выразим биссектрису СК через стороны АС и ВС, а также через угол С.

$CK=\frac{2*AC*BC*\cos\frac{\angle C}{2}}{AC+BC}.\quad(**)$

Теперь рассмотрим треугольник АМС. Там биссектрисой уже будет СО. Выразим СО по той же формуле биссектрисы

$CO=\frac{2AC*MC*\cos\frac{\angle C}{2}}{AC+MC}.$

По условию задачи MC=0,5ВС. Подставим это значение в предыдущую формулу

$CO=\frac{2AC*0,5*BC*\cos\frac{\angle C}{2}}{AC+0,5BC},$

$CO=\frac{AC*BC*\cos\frac{\angle C}{2}}{AC+0,5BC}.\quad(**)$

По условию задачи

$\frac{CO}{OK}=\frac{5}{3}.$

Пусть СО=5х, тогда ОК=3х. СО+ОК=5х+3х=8х.

$\frac{CO}{CK}=\frac{5x}{8x}=\frac{5}{8}$

$CO=\frac{5}{8}CK.\quad(***)$

Теперь в формулу (***) подставим значение СО из (**), значение СК из (*)

$\frac{AC*BC*\cos\frac{\angle C}{2}}{AC+0,5BC}=\frac{5}{8}\frac{2AC*BC*\cos\frac{\angle C}{2}}{AC+BC}$

Cократим обе части равенства на множители $AC*BC*\cos\frac{\angle C}{2}$

Получается

$\frac{1}{AC+0,5BC}=\frac{5}{8}\frac{2}{AC+BC}$

$\frac{1}{AC+0,5BC}=\frac{5}{4}\frac{1}{AC+BC}$

Умножим обе части на 4.

$\frac{4}{AC+0,5BC}=\frac{5}{AC+BC}$

Умножим обе части на (АС+ВС)*(AC+0,5BC).

4*(АС+ВС)=5*(AC+0,5BC)

4АС+4ВС=5АС+2,5ВС

4ВС-2,5ВС=5АС-4ВС

1,5ВС=АС

$\frac{AC}{BC}=1,5$

По-другому

$\frac{AC}{BC}=\frac{3}{2}$

Ответ:

$\frac{AC}{BC}=\frac{3}{2}$

bearcab_zn (114k баллов) 12 Март, 18