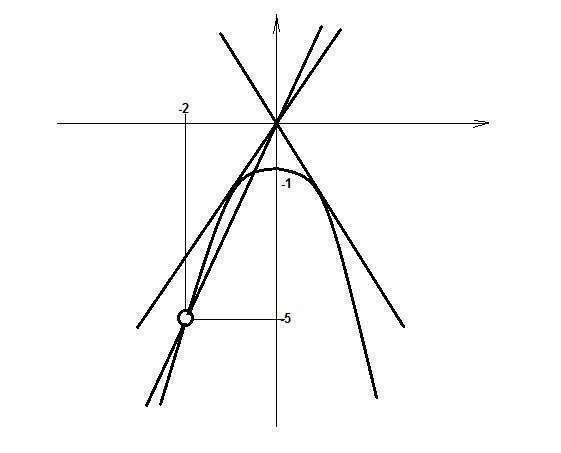
Это обыкновенная парабола, но в начальной формуле знаменатель
-x - 2 = -(x + 2), поэтому x ≠ -2. Это устранимый разрыв.
Поэтому у параболы выколота точка (-2; -5).
Прямые y = kx, которые пересекают эту параболу в 1 точке:
1) Касательная к параболе, имеющая уравнение:
f(x) = y0 + y'(x0)*(x - x0) = -x0^2 - 1 - 2x0*(x - x0) = -2x0*x - x0^2 - 1 + 2x0^2 = kx
x0^2 - 1 = 0
Точки касания двух касательных:
x0 = -1; k1 = -2; y0 = -1 - 1 = -2
x0 = 1; k2 = 2; y0 = -1 - 1 = -2
2) Прямая, проходящая через точку разрыва (-2; -5)
y = kx
-5 = k*(-2)
k = (-5)/(-2) = 5/2 = 2,5
Точка пересечения этой прямой и параболы:
2,5x = -x^2 - 1
x^2 + 2,5x + 1 = 0
2x^2 + 5x + 2 = 0
(2x + 1)(x + 2) = 0
x0 = -1/2; y0 = x0^2 - 1 = -1/4 - 1 = -5/4 - точка пересечения
x0 = -2; y0 = -x^2 - 1 = -4 - 1 = -5 - точка разрыва
Ответ: (x0; y0; k) = (-1; -2; -2); (1; -2; 2); (-1/2; -5/4; 5/2)