Высота правильной четырехугольной пирамиды равна 12 см, а апофема 15 см вычислить площадь...

$SO=12;\,\,\,\,SK=15$

Выпишем формулу для нахождения площади полной поверхности пирамиды.
$S=S_o+S_b$ , где $S_o$ - площадь основания, а $S_b$ - площадь боковой поверхности.

Итак, приступим.
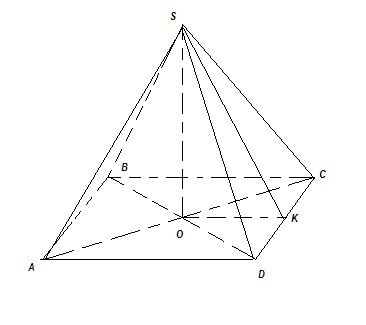
Найдем радиус вписанной окружности основания.
С треугольника $SOK$ по т. Пифагора найдем $OK.$
$SK^2=SO^2+OK^2\\ OK= \sqrt{SK^2-SO^2} = \sqrt{15^2-12^2} =9$

В основе лежит квадрат(т.к. пирамида ПРАВИЛЬНАЯ), значит можем найти стороны квадрата $ABCD$

$AB=2r=2\cdot OK=18$ см

Найдем площадь основания
$S_o=AB^2=18^2=324$ см²

Площадь боковой поверхности:
$S_b= \frac{1}{2}\cdot SK\cdot P_o$ , где $P_o$ - периметр основания

$S_b= \frac{1}{2} \cdot15\cdot4\cdot18=540$ см²

Осталось найти площадь полной поверхности

$S=S_o+S_b=324+540=864$ см²

Ответ: $864$ см².