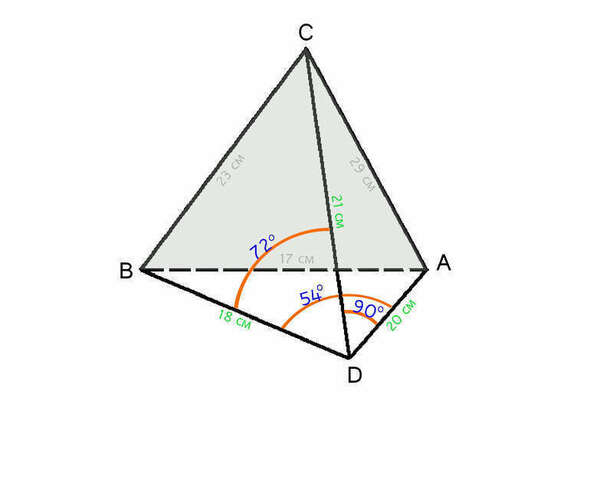
Рассмотрим боковую грань CDB как Δ. Известны 2 стороны этого Δ-ка и угол между ними. Найдём третью сторону BC при помощи теоремы косинусов:
BC= √ (DB²+DC² - 2×DB×DC × cos72°) =√ (324+441 - 2× 18 ×21 × 0,309) = √ 531,396 = 23 см
По той же теореме косинусов расчёта треугольника по 2м сторонам и углу между ними находим сторону AB Δ-ка ABD
АВ=√ ( 18² +20² - 2 × 18 ×20 × сos54°) = √ (324+400 - 720 × 0,5878) = √ 300,784 ≈ 17 см
По теореме Пифагора вычислим третью сторону основания тетраэдра - АС - она же гипотенуза прямоугольного треугольника АDC
АС=√ (21² + 20²) = 29 см
Таким образом мы нашли все рёбра основания АВС......
Теперь, зная длины всех рёбер (стороны всех треугольников тетраэдра), мы можем вычислить площадь любой грани по формуле Герона : S = √ ( p × (p-a) × (p-b) × (p-c), где a, b и c - длины сторон, а p - полупериметр, то есть 1/2 суммы всех сторон.
Начнём с площади DCB. p = (18+21+23):2 = 31 S= √ (31 ×(31-18)× (31-21)× (31-23)) = 179,5 см²
Продолжим с площадью ABD. p = (20+17+18) : 2 = 27,5 S = √ (27,5×(27,5-20)×(27,5-17)×(27,5-18))=√20573,4375 = 143,4 см²
Площадь ADC вычисляется проще, так как это прямоугольный Δ. S = 21×20 : 2 = 210 см ²
(Площадь грани ABC, которая по условию задачи является основанием тетраэдра, вычисляется всё по той же формуле Герона: квадратный корень из произведения полупериметра треугольника и разностей полупериметра с каждой из сторон. p = (23+17+29) : 2= 34,5 S=√ (34,5 × (34,5-17)×(34,5-23)×(34,5-29))= √38187,1875=195,4 см²)
ВСЁ! Надеюсь, в расчётах ничего не напутал.