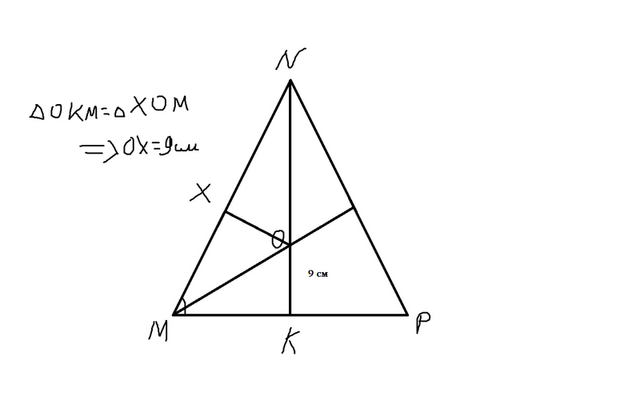1.Решите уравнение: а)2х+3=0 2.В остроугольном треугольнике MNP биссектриса угла М...

Question

Дано ответов: 2

Mousesk_zn · Answer 1 · 2018-03-12T03:06:40+0000

1.
2x+3=0
2x=-3
x= $-\frac{3}{2}$

2.

расстояние от О до МN-это перпендикуляр ОH

рассмотрим 2 треуг-ка MHO и MKO ; они прямоугольные углы H и К -прямые

МО- общая сторона и угол НМО=углуОМК , т.к. МО- биссектр.

треуг.равны по гипотенузе и острому углу, тогда НО=ОК=9

000LeShKa000_zn · Answer 2 · 2018-03-12T03:06:41+0000

1) Преобразуем уравнение:

$2x=-3 \\ x=-1,5$

2)Рассмотрим остроугольный треугольник MNK. У нас есть биссектриса одного угла M. Назову его MC. NK является высотой (я, лично, провел ее вниз, я тебе рисунок скинул во вложениях), следовательно, образуется треугольник OKM. В условии сказано найти расстояние от O до MN. Слово "расстояние" эквивалетно слову "перпендикуляр". Вот и проводим высоту от точки O до MN (высоту назовем OX). Снова образуется прямоугольный треугольник XOM. Треуголник OKM равен XOM потому, что гипотенуза и прилежащий угол равны, следовательно, расстояние равно 9 см.