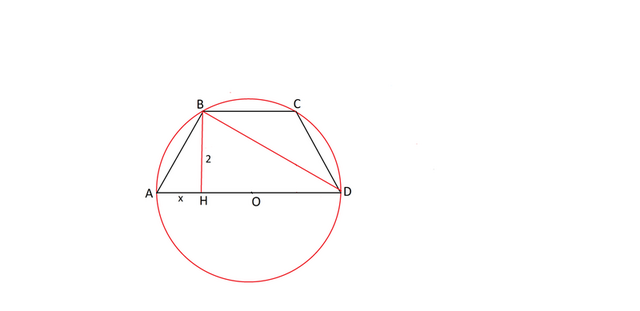
Сделаем рисунок согласно условию задачи.
Проведем в трапеции высоту ВН и диагональ ВD.
Так как АD - диаметр окружности, в которую трапеция вписана,
треугольник АВD- прямоугольный ( угол АВD опирается на дугу 180 градусов).
Площадь трапеции равна произведению ее высоты на полусумму оснований.
S ABCD=BH(BC+AD):2
2S=BH(BC+AD)
(BC+AD)=2S:BH
(BC+AD)=16:2=8
--------------------------------------------------------
Высота равнобедренной трапеции, проведенная из вершины тупого угла, делит большее основание на два отрезка, меньший из которых равен полуразности оснований, а больший – полусумме оснований.
--------------------------------------------------------
Обозначим отрезок АН =х, а
НD= полусумме оснований и равен 4
-------------------------------------------------------
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой..
------------------------------------------------------
Cледовательно,
ВН²=АН*НD
4=4х
х=1
AD=1+4=5
R=AO=5:2=2,5