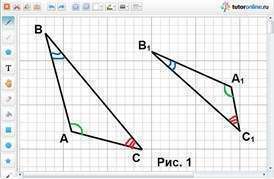
{Рисунок во вложении.}
Подобные треугольники —треугольники , у которых углы соответственно равны, а стороны одного пропорциональны сходственным сторонам другого треугольника.
Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными. Так, на рисунке стороны AB и A1B1, AC и A1C1, BC и B1C1, сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A1B1C1.
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия.
Углы A = A1, B = B1, C = C1 и AB/A1B1 = ВC/В1C1 = АС/А1С1 = k, где k – коэффициент подобия. И на рисунке видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.