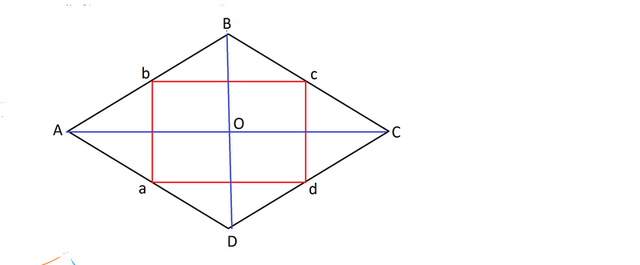
Сделаем рисунок.
Проведем диагонали ВD и АС ромба.
Соединим середины сторон a,b,c,d попарно.
Получившийся четырехугольник - прямоугольник, т.к. его стороны, являясь средними линиями треугольников, на которые делит ромб каждая диагональ - параллельны диагоналям ромба - основаниям этих треугольников.
А диагонали ромба пересекаются под прямым углом,
и поэтому углы четырехугольника также прямые.
Сумма углов параллелограмма ( а ромб - параллелограмм), прилегающих к одной стороне, равна 180°
Так как тупой угол ромба равен 120°, острый равен 60°
Пусть меньшая диагональ d, большая -D
Диагональ d равна стороне ромба, так как образует с двумя сторонами ромба равносторонний треугольник ABD с равными углами 60° .
Большая диагональ D в два раза длиннее высоты АО равностороннего треугольника AB.
АО равна стороне ромба АВ, умноженной на синус угла 60°
АО=4√3:2=2√3
D=АС=4√3
Стороны прямоугольника ( на рисунке красного цвета) равны:
ширина ab равна половине BD и равна 2 см
длина bc равна половине АС и равна 2√3 см
S abcd=2*2√3=4√3