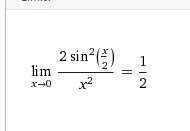Преобразуем выражение, стоящее под знаком предела:
Числитель:
2*sin (x/2)*sin(x/2)
Знаменатель:
4*(x/2)*(x/2)
Используем замечательный предел: При x→0 lim ( sin(x/2) / (x/2) ) = 1
Получаем:
2*sin(x/2)*sin(x/2) / (4*(x/2)*(x/2))
2*1*1 / 4 = 1/2
Ответ: 1/2
Проверим наше решение программно:
См. скрин:
Ответы совпали, значит наше решение - правильное!