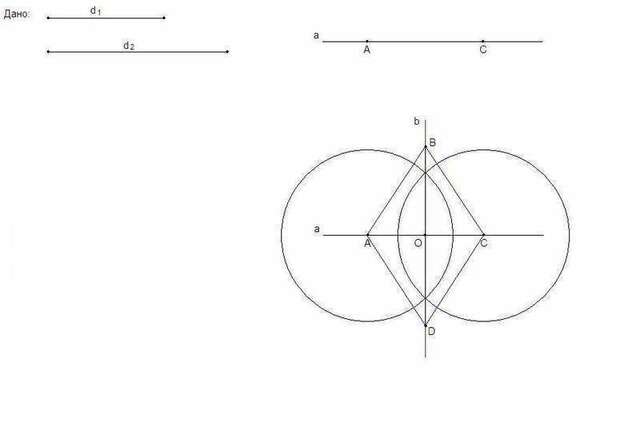
Построение ромба по двум диагоналям.
1. На прямой а отложим отрезок АС, равный данной диагонали d₁.
2. Проведем серединный перпендикуляр к отрезку АС. Для этого построим две окружности одинакового произвольного радиуса (большего половины АС) с центрами в точках А и С. Через точки пересечения окружностей проведем прямую b.
b∩a = O.
O - середина АС.
3. Точно так же разделим данную диагональ d₂ пополам. На прямой b от точки О отложим отрезки ОВ и OD, равные половине диагонали d₂.
ABCD - искомый ромб.
Построение ромба по стороне и углу.
1. На прямой а отложим отрезок KN, равный данному отрезку АВ.
2. Построим ∠TKN = ∠PNN' = ∠CDE. Для этого проведем дугу произвольного одинакового радиуса с центрами в точках D, К и N.
Точки пересечения дуг с прямой а обозначим K' и N' (эти точки находятся по разные стороны от точки N).
Измерим
расстояние C'E' и таким радиусом проведем окружности с центрами в
точках K' и N'. Через точки пересечения этих окружностей с ранее
построенными дугами проведем лучи КТ и NP.
3. На лучах КТ и NP отложим отрезки KL и NM соответственно, равные данному отрезку АВ.
4. Соединим точки L и М.
KLMN - искомый ромб.
Доказательство:
KL║NM так как соответственные углы LKK' и MNN' равны по построению.
KL = NM по построению, значит KLMN - параллелограмм.
Смежные стороны его равны, значит это ромб.