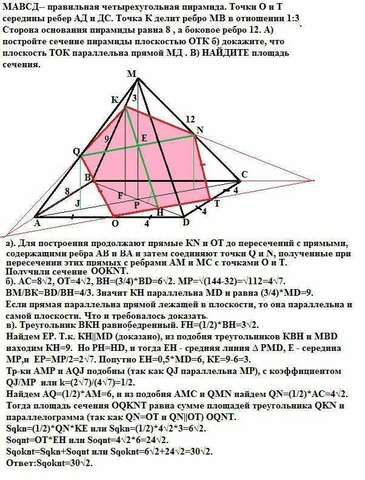
А). Построение понятно из рисунка.
б). АС=8√2, ОТ=4√2, ВН=(3/4)*BD=6√2. МР=√(144-32)=√112=4√7.
ВМ/ВК=ВD/BH=4/3. Значит КН параллельна МD и равна (3/4)*MD=9.
Если прямая параллельна прямой лежащей в плоскости,
то она параллельна и самой плоскости.
Что и требовалось доказать.
в). Треугольник ВКН равнобедренный. FH=(1/2)*BH=3√2.
Найдем ЕР. Т.к. КН||МD (доказано), из подобия треугольников КВН и МВD
находим КН=9. Но РН=НD, и тогда ЕН - средняя линия ∆ РМD,
Е - середина МР, и ЕР=МР/2=2√7. Попутно ЕН=0,5*MD=6, КЕ=9-6=3.
Тр-ки АMP и AQJ подобны (так как QJ параллельна МР), с коэффициентом QJ/MP или k=(2√7)/(4√7)=1/2.
Найдем AQ=(1/2)*AM=6, и из подобия AMC и QMN найдем QN=(1/2)*АС=4√2.
Тогда площадь сечения OQKNT равна сумме площадей треугольника
QKN и параллелограмма (так как QN=ОТ и QN||ОТ) OQNT.
Sqkn=(1/2)*QN*KE или Sqkn=(1/2)*4√2*3=6√2.
Soqnt=OT*EH или Soqnt=4√2*6=24√2.
Sqoknt=Sqkn+Soqnt или Sqoknt=6√2+24√2=30√2.
Ответ:Sqoknt=30√2.