Сторона основания правильной треугольной пирамиды равна 6, а боковое ребро образует с...

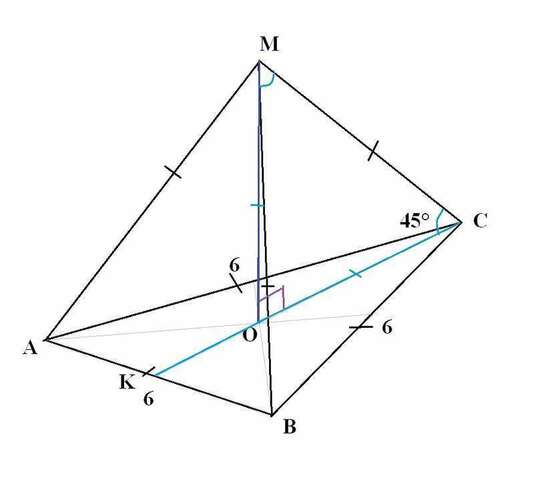
Объем пирамиды

$V=\frac{1}{3}S_{ABC}H$

Т.к. ∆АВС - правильный, то его площадь

$S_{ABC}=\frac{AB^2\sqrt3}{4}=\frac{6^2\sqrt3}{4}=9\sqrt3$

Основание О высоты МО правильной пирамиды - центр описанной и вписанной окружностей. В правильном ∆СКВ СК - медиана, биссекториса, высота.

В ∆СКВ КВ=3, ∠СВК=60°, СК = СВsin60°=6·√3/2=3√3

О - точка пересечения медиан ∆АВС, СО=2СК/3=2√3

Высота МО⊥(АВС), тогда МО⊥CO. ∆МОС - прямоугольный и ∠МСО=45°, значит и ∠СМО=45°. Значит, ∆МОС - равнобедренный, тогда СО=МО =2√3.

Таким образом,

$V=\frac{1}{3}S_{ABC}H=\frac{1}{3}*9\sqrt3*2\sqrt3=18$