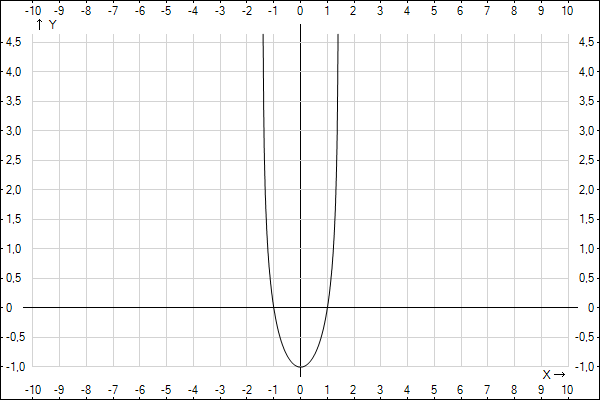
0, x^2-2<0, (x+\sqrt2)(x-\sqrt2)<0, -\sqrt2<x<\sqrt2, \\ D_g=(-\sqrt2;\sqrt2), \\ g'(x)=(2-x^2)\ln0,5\cdot(2-x^2)'=-2x(2-x^2)\ln0,5= \\ =2x(x^2-2)\ln0,5, \\ g'(x)=0, 2x(x^2-2)\ln0,5=0, \\ x(x+\sqrt2)(x-\sqrt2)=0, \\ x_1=0, x_2=-\sqrt2\notin D, x_2=\sqrt2\notin D, \\ g(0)=\log_{2^{-1}}2=-\log_22=-1, \\ min - (0;-1), g_{min}=-1." alt="g(x)=\log_{0,5}(2-x^2), \\ 2-x^2>0, x^2-2<0, (x+\sqrt2)(x-\sqrt2)<0, -\sqrt2<x<\sqrt2, \\ D_g=(-\sqrt2;\sqrt2), \\ g'(x)=(2-x^2)\ln0,5\cdot(2-x^2)'=-2x(2-x^2)\ln0,5= \\ =2x(x^2-2)\ln0,5, \\ g'(x)=0, 2x(x^2-2)\ln0,5=0, \\ x(x+\sqrt2)(x-\sqrt2)=0, \\ x_1=0, x_2=-\sqrt2\notin D, x_2=\sqrt2\notin D, \\ g(0)=\log_{2^{-1}}2=-\log_22=-1, \\ min - (0;-1), g_{min}=-1." align="absmiddle" class="latex-formula">
