Площадь бок. поверхности сферы=4*пи*R^2, где r- радиус сферы.
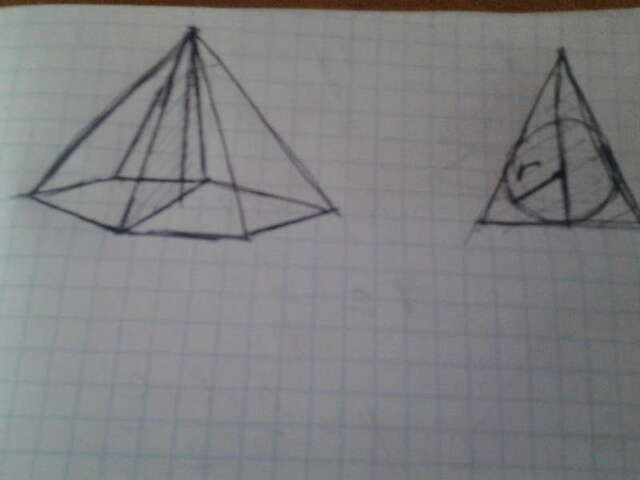
Центральное сечение пирамиды-равнобедренный треугольник. Найдем радиус вписанной в треугольник окружности.
r=Sтреугольника/ p, p-полупериметр.
Площадь треугольника=1/2*основание*высоту
Высота треугольника=Высоте пирамиды= 2 корней из 10
Основание найдем по теореме Пифагора
(половина основания)^2=12
Основание=4 корня из 3
Площадь треугольника=0, 5*4 корня из 3* 2 корней из 10=4*корень из 30
Полупериметр=(2 корня из13+2 корня из13+4 корня из 3)/2=2 корня из13+2 корня из 3
Радиус вписанной в треугольник окружности=4*корень из 30/(2 корня из13+2 корня из 3)=2*корень из 30/(корень из 13+корень из 3)= радиус сферы.
Площадь бок. поверхности сферы=4*пи*(2*корень из 30/(корень из 13+корень из 3))^2=4*пи*120/(16+2*корень из 39)=240*пи/(8+корень из 39)