Висота рівнобедриного трикутника проведена до основи дорівнює 8 см а радіус описаного...

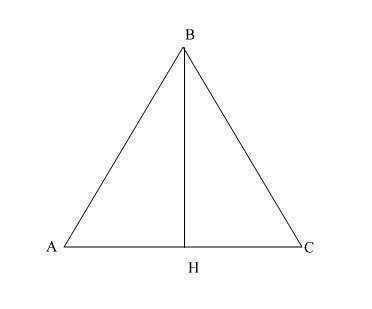
Дан равнобедренный треугольник АВС с высотой ВН = 8 см.

Радиус описанной окружности равен R = 13 см.

Пусть сторона АВ=ВС=а, а основание АС=b.

$R = \frac{a^{2}}{\sqrt{(2a)^{2}-b^{2}}} \\$

Рассмотрим треугольник АНВ - прямоугольный.

AB^2 = BH^2 + AH^2 или $a^{2} = 64 + \frac{1}{4}b^{2}$

Подставим в формулу для радиуса.

$13 = \frac{64+\frac{1}{4}b^{2}}{\sqrt{(2\sqrt{64+\frac{1}{4}b^{2}})^{2}}-b^{2}} \\ 13 = \frac{64+\frac{1}{4}b^{2}}{16} \\ 64 + \frac{1}{4}b^{2} = 13*16 \\ b=24$

AC = 24, следовательно, АН = 12.

АВ^2 = AH^2 + BH^2

$AB = \sqrt{208} = 4\sqrt{13}$