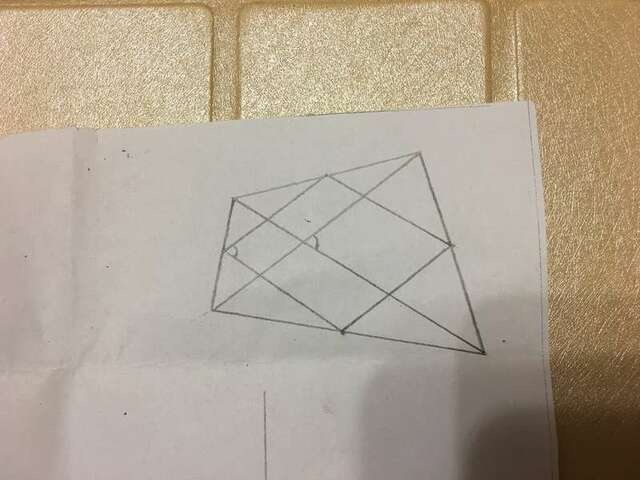
Каждая из сторон нового четырёхугольника - это средняя линия в соответствующем треугольнике, отсечённом диагоналями данного четырёхугольнике, значит новые стороны параллельны диагоналям, значит малый четырёхугольник - параллелограмм (это для справки).
Площади малых треугольников, отсечённых средними линиями в треугольниках с диагоналями в основании, равны одной четвёртой площадей этих треугольников (при коэффициенте их подобия k=2, коэффициент подобия их площадей k²=4).
Посчитаем площади отсечённых треугольников.
Обозначим площади треугольников с основаниями, лежащими на диагонали d₁ как S1 и S2, а треугольников с основаниями на диагонали d₂ как S3 и S4. площадь большого четырёхугольника обозначим S.
S=S1+S2 и S=S3+S4.
Площади отсечённых треугольников в первой паре: Sотс1=(S1+S2)/4=S/4.
Площади отсечённых треугольников во второй паре: Sост2=(S3+S4)/4=S/4.
Площади всех отсечённых треугольников: Sост=Sотс1+Sотс2=S/4+S/4=S/2.
Итак, площадь малого четырёхугольника: s=S-Sотс=S-S/2=S/2 - это ответ.
Можно немного проще.
Площадь произвольного четырёхугольника: S=(1/2)d₁·d₂·sinα, где α - угол между диагоналями.
Стороны малого четырёхугольника равны половинам диагоналей (мы это уже доказали).
Угол между соответственно параллельными прямыми равны, значит указанный угол между сторонами малого четырёхугольника равен α.
Площадь малого четырёхугольника (параллелограмма): s=ab·sinα=(d₁/2)·(d₂/2)·sinα=(1/4)d₁·d₂·sinα=S/2.
Всё!