1. Треугольник АВС задан координатами своих вершин в прямоугольной декартовой системе...

Question

1. Треугольник АВС задан координатами своих вершин в прямоугольной декартовой системе координат. А(3, 0), В(-1, 4), С(6, 3); Вычислить: а) длины сторон; б) углы; в) площадь; г) длины биссектрисы, медианы и высоты, проведенных из вершины А; д) радиусы и центры вписанной и описанной окружностей.

Answer 1

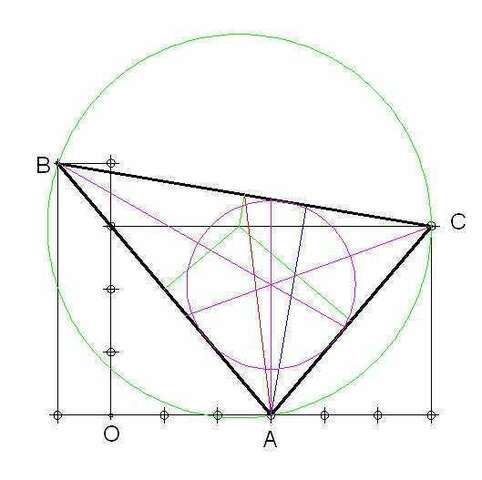
РАСЧЕТ ТРЕУГОЛЬНИКА
заданного координатами вершин:
 Вершина 1: A(3; 0)
 Вершина 2: B(-1; 4)
 Вершина 3: C(6; 3)
 
ДЛИНЫ СТОРОН ТРЕУГОЛЬНИКА
 Длина BС (a) = 7,07106781186548
 Длина AС (b) = 4,24264068711928
 Длина AB (c) = 5,65685424949238
 
ПЕРИМЕТР ТРЕУГОЛЬНИКА
 Периметр = 16,9705627484771
 
ПЛОЩАДЬ ТРЕУГОЛЬНИКА
 Площадь = 12
 
УГЛЫ ТРЕУГОЛЬНИКА
 Угол BAC при 1 вершине A:
   в радианах = 1,5707963267949
   в градусах = 90
 Угол ABC при 2 вершине B:
   в радианах = 0,643501108793284
   в градусах = 36,869897645844
 Угол BCA при 3 вершине C:
   в радианах = 0,927295218001612
   в градусах = 53,130102354156
 
ЦЕНТР ТЯЖЕСТИ
 Координаты Om(2,66666666666667; 2,33333333333333)
 
ВПИСАННАЯ ОКРУЖНОСТЬ
 Центр Ci(3; 2)
 Радиус = 1,4142135623731
 
ОПИСАННАЯ ОКРУЖНОСТЬ
 Центр Co(2,5; 3,5)
 Радиус = 3,53553390593274
 
МЕДИАНЫ ТРЕУГОЛЬНИКА
 Медиана АM1 из вершины A:
   Координаты M1(2,5; 3,5)
   Длина AM1 = 3,53553390593274
 
ВЫСОТЫ ТРЕУГОЛЬНИКА
 Высота AH1 из вершины A:
   Координаты H1(3,48; 3,36)
   Длина AH1 = 3,39411254969543

---