Основание прямой призмы - треугольник со стороной А, противолежащим этой стороне углом...

Question

Основание прямой призмы - треугольник со стороной А, противолежащим этой стороне углом альфа и прилежащим углом бетта. Диагональ боковой грани, содержащей сторону основания, к которой прилегают углы альфа и бетта, наклонена к плоскости основания под углом гамма. Найдите высоту призмы.

Answer 1

..................................

---

Answer 2

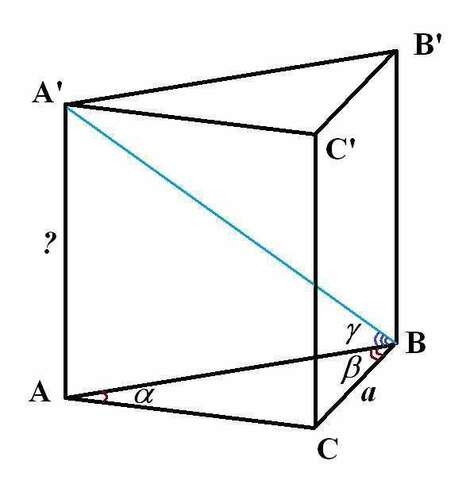
Чертеж во вложении.

По теореме о сумме углов треугольника в ∆АВС ∠С=180-(α+β).

В ∆АВС по теореме синусов

\ \ AB=\frac{BC*sin C}{sin A}=\frac{a*sin (180^o-(\alpha+\beta))}{sin\ \alpha}=\frac{a*sin (\alpha+\beta)}{sin\ \alpha}." alt="\frac{AB}{sinC}=\frac{BC}{sinA} \ \ => \ \ AB=\frac{BC*sin C}{sin A}=\frac{a*sin (180^o-(\alpha+\beta))}{sin\ \alpha}=\frac{a*sin (\alpha+\beta)}{sin\ \alpha}." align="absmiddle" class="latex-formula">

В прямоугольном ∆А'AВ 

\ \ AA' = AB* tg\ B = \frac{a*sin (\alpha+\beta)}{sin\ \alpha}*tg\ \gamma" alt="\frac{AA'}{AB}=tg\ B \ \ => \ \ AA' = AB* tg\ B = \frac{a*sin (\alpha+\beta)}{sin\ \alpha}*tg\ \gamma" align="absmiddle" class="latex-formula">

Ответ: 

---