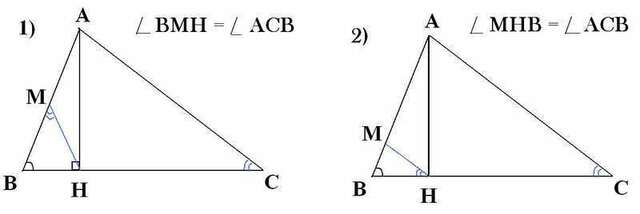
Чертежи к задаче - во вложении.
По условию задачи в силу подобия треугольников АВС и ВМН необходимо рассмотреть 2 случая.
1-й случай.
Из подобия треугольников следует равенство ∠АВС=∠MBH (по условию) и ∠АСВ=∠ВMН.
Тогда отношение сходственных сторон:
По теореме косинусов в ∆АВС АС²=АВ²+ВС²-2·АВ·ВС·cos B=18²+16²-2·18·16·4/9=18²+16²-16²=18² => AC=18
В прямоугольном ∆АНВ ВН=АВcosB= 18·4/9=8
Тогда получим
\frac{MH}{18}=\frac{8}{18} \ => MH=8" alt="\frac{MH}{AC}=\frac{BH}{AB} \ => \frac{MH}{18}=\frac{8}{18} \ => MH=8" align="absmiddle" class="latex-formula">
2-й случай.
Из подобия треугольников следует равенство ∠АВС=∠MBH (по условию) и ∠АСВ=∠MНB.
Тогда MH||AC и отношение сходственных сторон:
\frac{MH}{18}=\frac{8}{16}\ => MH=\frac{18*8}{16}=9" alt="\frac{BM}{BA}=\frac{MH}{AC}=\frac{BH}{BC} \ => \frac{MH}{18}=\frac{8}{16}\ => MH=\frac{18*8}{16}=9" align="absmiddle" class="latex-formula">
Ответ: 8 или 9.
