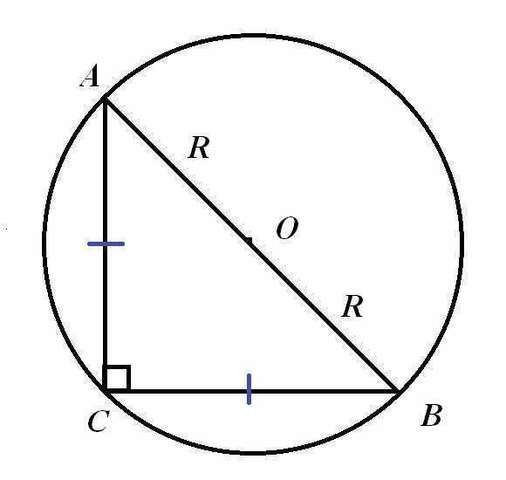
Пусть окружность с центром О описана около прямоугольного равнобедренного треугольника АВС (∠С=90°). Тогда вписанный в окружность угол С опирается на дугу АС=2*90°=180°. Значит, хорда АВ - диаметр окружности. Поэтому точка О делит гипотенузу АВ пополам.
Из длины окружности найдем радиус:
С=2ПR
8П=2ПR
R=4.
Тогда АВ=2*4=8.
По теореме Пифагора АВ²=АС²+ВС². По свойству равнобедренного треугольника АС=ВС.
Тогда АВ²=2АС²

Для прямоугольного треугольника