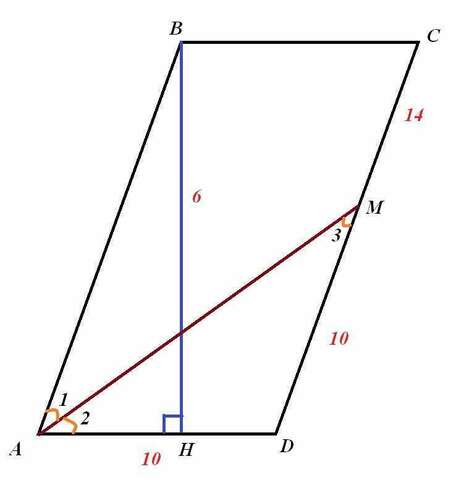
Чертеж во вложении.
В параллелограмме большая высота проходит перпендикулярно меньшей стороне.
Пусть АМ - биссектриса ∠А, которая пересекает сторону СD в точке М:
DМ=10, МС=14.
По определению биссектрисы ∠1 =∠2, еще ∠1 = ∠3(накрестлежащие), значит, ∠2 = ∠3.
Тогда ∆АМD - равнобедренный с основанием АМ. Поэтому АD=DМ=10.
Площадь параллелограмма S = BH*AD = 6*10=60.