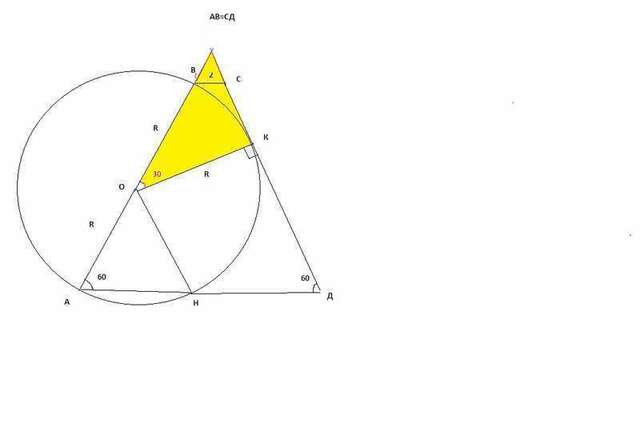
Ух ты, какая задачка.
Смотри файл и здесь решаем.
АО=ОН (радиус), и угол 60, тогда треугольник АОН - равносторонний.
ОН ║СД (угол Н и Д - по 60 градусов.)
т.к. ОК ⊥СД ⇒ ОК⊥ОН ⇒ ∠ВОК=30
А теперь делаем "финт ушами" - достраиваем красный треугольник.Он равносторонний со стороной 2. И рассматриваем желтый прямоугольный треугольник с углом 30 градусов.
У него гипотенуза R+2, катеты R и (R+2)/2
по т. Пифагора
(R+2)²=R²+((R+2)/2)²
раскрывая скобки, получаем
R²-12R-12=0
решая, получаем один положительный ответ- R=6+4√3
сторона АВ = 2R= 12+8√3
Конечно, можно найти высоту и найти площадь классическим методом, но оно нам надо?
Мы идем другим путем- делаем второй "финт ушами"
Площадь трапеции равна площади большого равностороннего треугольника со стороной 2R+2 и минус площади маленького со стороной 2
S=((12+8√3+2)²*sin60)/2 - (2²*sin60)/2=... делаем преобразования...=168+96√3