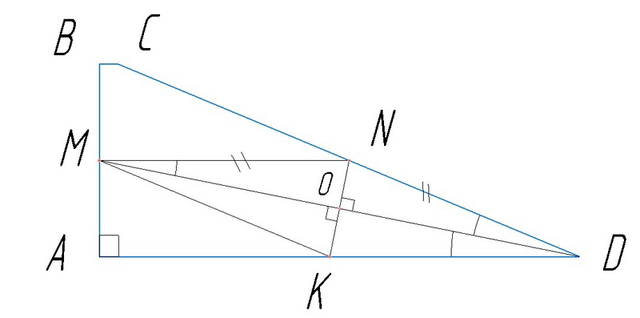
Дано: АВCD - трапеции, АВ и CD - боковые стороны трапеции
АВ =10, CD = 26, ВС = 1, DM - биссектриса ∠ADC проходящая через середину АВ.
Найти: S - ?
Решение.
Проведем через точку М линию MN ║ AD, т.к. АМ=МВ= 10 / 2 = 5 по условию задачи, то MN - средняя линия.
DM - биссектриса, то ∠ADM = ∠MDC, а ∠NMD = ∠ADM как накрест лежащие при параллельных прямых (MN ║ AD), отсюда следует, что ∠NMD = ∠NDM следовательно ΔMND - равнобедренный. (смотри рисунок ниже)
тогда
MN = ND = CD / 2 = 26 / 2 = 13
С другой стороны средняя линия в трапеции равна

Проведем в равнобедренном треугольнике ΔMND прямую NO - высоту и продлим эту прямую до точки К лежащей на прямой AD.
ΔNOD = ΔKOD - по стороне (OD) и двум прилежащим к ней углам, следовательно MNDK ромб, у которого
MK = MN = ND = KD = 13
тогда
AK = AD - KD = 25 - 13 = 12
Если в ΔAMK выполняется условие MK² = AM² + AK² , то ΔAMK - прямоугольный.
13² = 5² + 12²
169 = 169 , следовательно ∠MAK = 90° , а трапеция ABCD прямоугольная,
Тогда высота трапеции равна
h = AB = 10
Найдем площадь трапеции
 кв.ед.
кв.ед.
Ответ: S = 130 кв.ед.