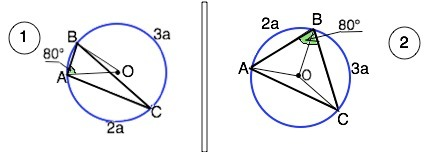
1) В ∆ АОВ стороны АО=ВО – радиусы.
∆ АОВ равнобедренный, ∠ОАВ=∠ОВА=80° ⇒ ∠АОВ= 180°-2•80°=20°
Полная окружность содержит 360° ⇒ дуга АСВ=360°-20°=340° и содержит 2а+3а= 5а частей.
а=340°:5=68°
Дуга АС=2•68°=136° Вписанный ∠АВС=136°:2=68°
Дуга ВС=3•68°=204° Вписанный ∠ВАС=102°
Вписанный ∠АСВ равен половине центрального АОВ и равен 10°.
Ответ: ∠АВС=68°
∠ВАС=102°
∠АСВ = 10°.
* * *
В ∆ АВС ∠АВС=80° равен половине градусной меры дуги, стягиваемой хордой АС.
Дуга АС=2•80°=160°
Тогда дуга АВС=360°-160°=200° и содержит 5а частей.
а=200°:5=40°
Дуга ВС=3•40°=120° ⇒Вписанный ∠ВАС=120°:2=60°
Дуга АВ=2•40°=80°. ⇒ Вписанный ∠АСВ=80°:2=40°
В ∆ АОВ центральный ∠АОВ опирается на дугу АВ и равен 80°.
∆ АОВ равнобедренный, углы при основании равны (180°-80°):2=50°
Ответ: 50°, 50°, 80°.