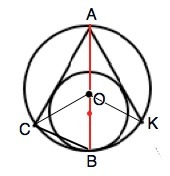
Отрезки касательных к окружности, проведённых из одной точки, не лежащей на окружности, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности. ⇒
∠САВ=∠КАВ=60°:2=30°
∠АСВ=∠АКВ=90°- опираются на диаметр АВ.
Прямоугольные ∆ АСВ=∆ АКВ по острому углу при А и общей гипотенузе АВ. ⇒
АС=AK=АВ•cos30°=2R*√3:2=R√3
* * *
Как вариант - СВ противолежит углу 30° и равен R, можно применить т.Пифагора,
или провести радиус ОС и находить АС из равнобедренного ∆ АОС по т.косинусов.