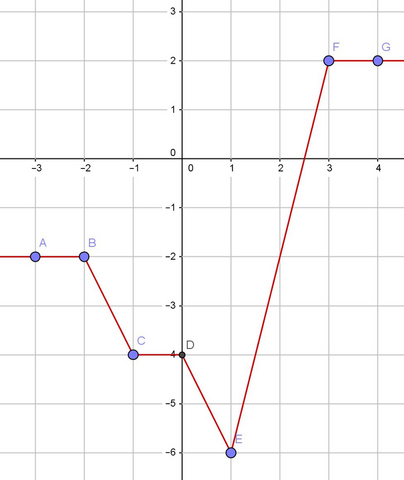
Мне не хочется раскрывать модули и решать кучу неравенств, проще сначала изобразить график функции y = |x + 1| - |x| + 3|x - 1| - 2|x - 3| - |x + 2| и решать неравенства там, где это имеет смысл.
Выражения под модулями меняют знак при x = -2, -1, 0, 1, 3; на каждом участке, где знаки не меняются, должен получиться отрезок прямой, кроме того, функция непрерывна. Поэтому имеет смысл просто взять по паре точек на каждом из отрезков и соединить их отрезками прямых.
x = -3: y = |-2| - |-3| + 3|-4| - 2|-6| - |-1| = 2 - 3 + 12 - 12 - 1 = -2
x = -2: y = |-1| - |-2| + 3|-3| - 2|-5| - |0| = 1 - 2 + 9 - 10 - 0 = -2
x = -1: y = |0| - |-1| + 3|-2| - 2|-4| - |1| = 0 - 1 + 6 - 8 - 1 = -4
x = 0: y = |1| - |0| + 3|-1| - 2|-3| - |2| = 1 - 0 + 3 - 6 - 2 = -4
x = 1: y = |2| - |1| + 3|0| - 2|-2| - |3| = 2 - 1 + 0 - 4 - 3 = -6
x = 2: y = |3| - |2| + 3|1| - 2|-1| - |4| = 3 - 2 + 3 - 2 - 4 = -2
x = 3: y = |4| - |3| + 3|2| - 2|0| - |5| = 4 - 3 + 6 - 0 - 5 = 2
x = 4: y = |5| - |4| + 3|3| - 2|1| - |6| = 5 - 4 + 9 - 2 - 6 = 2
График изображен на рисунке. По графику y >= 0 при x >= 5/2 (5/2 можно проверить, подставив в исходное неравенство. Действительно, y(5/2) = 0).
Ответ. x >= 5/2.