Я попробую доказать.
Итак, будем доказывать тот факт, что треугольники равны.
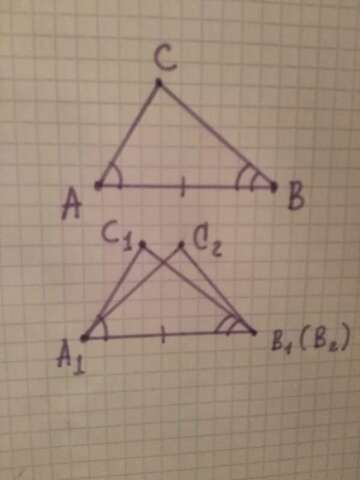
Пусть будет так, что A1B2C2- треугольник, равный треугольнику ABC, с вершиной B2 на луче A1B1 и вершиной C2 в той же полуплоскости как бы относительно прямой A1B1, где будет у нас находиться вершина C1.
Так как A1B2=A1B1, то вершина B2 совпадает с вершиной B1, это очевидно. Так как угол B1A1C2= углу B1A1C1 и тогда угол A1B1C2 = углу A1B1C1, то луч A1C2 будет совпадать с лучом A1C1, а луч B1C2 совпадает с лучом B1C1. Отсюда следует, что вершина C2 совпадает с вершиной C1...
Итак, треугольник A1B1C1 совпадает с треугольником A1B2C2, а как раз и значит,что он равен треугольнику ABC.
Теорема доказана.
Вот в прикреплённом файле есть мои чертежи по доказательству: