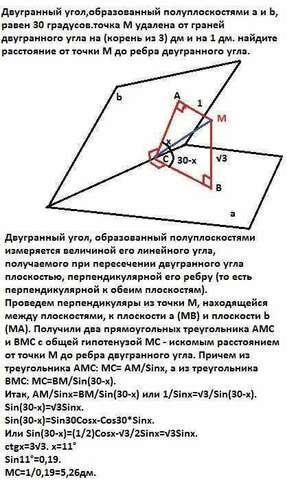
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям). Проведем перпендикуляры из точки М,
находящейся между плоскостями, к плоскости a (MB) и плоскости b (МА). Получили два прямоугольных треугольника АМС и ВМС с общей гипотенузой МС - искомым расстоянием от точки М до ребра
двугранного угла. Причем из треугольника АМС: МС= АМ/Sinx, а из треугольника ВМС: МС=ВМ/Sin(30-x).
Итак, АМ/Sinx=ВМ/Sin(30-x) или 1/Sinx=√3/Sin(30-x).
Sin(30-x)=√3Sinx.
Sin(30-x)=Sin30Cosx-Cos30*Sinx.
Или Sin(30-x)=(1/2)Cosx-√3/2Sinx=√3Sinx. Разделим обе части на √3Sinx.
ctgx=3√3. х=11° (по таблице)
Sin11°=0,19. Тогда
МС=1/0,19=5,26дм.
Ответ: МС=5,26дм.